Gradient, Divergence, Curl에 대하여.

고등학교때 익히 다루어왔던 미분은 스칼라 함수에 대하여 변화율을 적용한 것이다.

이것을 벡터함수에까지 확장한 개념이 위의 Gradient, Divergence, Curl이다.

시작을 벡터함수의 미분개념이구나 하고 이해하고 차차 살펴보자.

1. Gradient

단도직입적으로 스칼라함수의 미분이다. 기호로는 ▽ 라고 나타낸다.

중력과같은 포텐셜을 가지는 것을 보존력(Conservative Force)이라고 하는데,

여기서 포텐셜을 U라 하면, 중력 F는 F = -▽U 으로 구해진다.

간단하게 예를들면, 질량이 M인 물체의 중력장에 질량m인 물체가 r과의 거리만큼 떨어져있을때 그 지점의 포텐셜은

U = -GMm/r  으로 구해지며 이를 r로 미분한 GMm/r² 이 그 지점에서의 힘인 것을 알 수있다.

즉, gradient는 이것을 3차원으로 확장한 것이다.

P = f(x,y,z) 로 표현되는 함수 P가 있을때, 이것의 gradient를 취한다는 것은,
P의 변화율을 나타낸 함수를 구한다는 것이다.

기하학적으로 이해해보자면 다음과 같다.

xyz축을 상상해보자.
xy평면 위쪽에 울퉁불퉁한 평면 T가 있다고 가정해보자. 그리고 그 평면 T를 z축이 관통할 것이다.

이때, 평면 T를 나타내는 벡터함수의 gradient를 취하면, 그 평면의 변화율이 구해진다.

여기서 함수 ▽T 의 최대값을 구한다는 뜻은, 경사가 가장 급격하게 변하는 점을 구한다는 것이다.
산에서 내려오는 등산로로 치면 가장 빠른 코스를 찾는다는 느낌 - ?

구체적인 계산법은 다음과 같다.

 

 

여기서 ▽에 벡터표시인 →를 붙인 이유는 마치 내적과 같은 형태를 하고 있기 때문이다. 

gradient가 x성분은 어떤 함수를 x로 편미분, y성분은 y로 편미분, z성분은 z로 편미분 한 벡터라고 생각하면,

▽P 라는건  이 gradient벡터와 스칼라 P의 곱인 셈이다.

그렇다면 만약 스칼라함수가 아니라 벡터함수의 경우는 미분이 어떻게 되는것인가 하는 생각이 들것이다.

여기서 Curl과 Divergence가 나오게 된다.

2. Divergence

기호로는 ▽·P처럼, 내적의 형태로 나타낸다.

즉, gradient와 유사하나 단지 divergence를 취하면 벡터함수가 스칼라함수로 변한다는 것을 알 수 있다.

 

 

3. Curl

curl은 마찬가지로 벡터함수에 취하는데 내적이 아니라 외적을 하게 된다.

즉, ▽×P 이며 다음과 같이 3×3 행렬식으로 나타낼수 있다.

 

이제 스칼라/벡터 함수의 세가지 미분법을 알아보았는데, 이계 미분도 정의할수 있을 것이다.

마찬가지로 스칼라→벡터, 벡터→스칼라, 벡터→벡터 세 가지 방법이 있을 것이다.

첫번째로, 원함수 P가 스칼라 함수라고 하면, Gradient인 ▽P만 가능하다.

gradient를 취한 ▽P는 벡터함수이므로 여기에 divergence나 curl 두 가지가 모두 가능하다.
그림으로 보면 이렇게 된다.

마찬가지로 원함수 P가 벡터함수라고 하면,
처음에 Divergence와 curl모두 가능하고,
각각의 경우에 대해 div-grad, curl-div, curl-curl이 가능하므로.. 

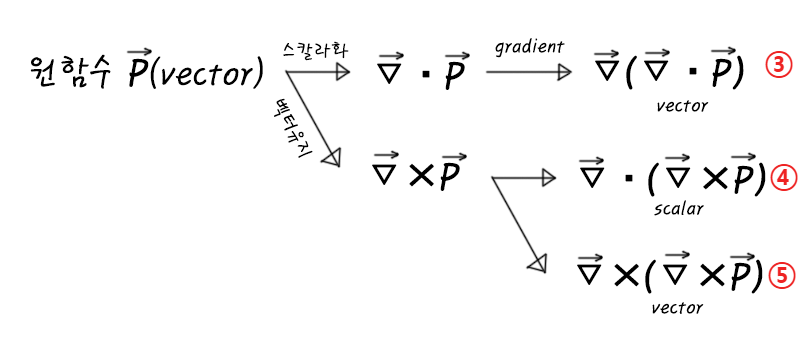
 이렇게 될 것이다.

즉, 어떠한 원함수 P에 대한 이계 미분은 총 5가지(스칼라P에서 2가지, 벡터P에서 3가지)경우가 있다.

이 중에서 특이한 성질을 가진 것들을 짚고 넘어가보자.

먼저, Laplacian이라는 새로운 operator를 정의한다.

divergence와 gradient를 중첩하여 실시한 경우로 기호로는 ▽² 으로 표기하며, vector laplacian과 scalar laplacian 두가지가 있다.
 
벡터 라플라시안은 말 그대로 벡터 원함수의 라플라시안을 취하는 것이고,
스칼라 라플라시안은 스칼라 원함수의 라플라시안이다.

 

주의 할 점은 같은 라플라시안이라도 두 가지의 차이점이 있는데,
스칼라 라플라시안의 경우는 먼저 grad를 취하고 다음 div를 취하는 것이다.(당연히 최종 결과는 스칼라)

함수 P의 각 성분을 P1, P2, P3라고 하고 수식으로 써보면

▽²P = P1xx + P2yy + P3zz 가 된다.
(*P1xx는 P1의 x에 대한 두번 편미분)

반면, 벡터 라플라시안은 먼저 div를 취하고 grad를 취하는 것이 아니라,(*주의 - 이 연산은 벡터 라플라시안이라고 칭하지 않는다. 그냥 벡터 함수의 div 연산후 grad 연산이다)

각 성분의 2계 미분을 하되, 벡터형을 그대로 남기는 것이다. 수식으로 써보면 다음과 같다.

▽²P = (P1xx, P2yy, P3zz)

결과값은 세 가지 성분을 가지는 벡터가 된다.


위에서 서술한 스칼라/벡터 라플라시안 두 가지 모두 기호는 ▽²P 가 된다. (원함수 P가 벡터일 경우는 ▽²P) 

위의 이계 미분 5가지 경우에서는 ②번이 스칼라 라플라시안임을 알 수있다. (*벡터 라플라시안은 위의 다섯가지 예 에서는 직접적으로 유도되지 않는다.)

다음으로, 값이 0이 나오는 case가 두 가지가 있다.
바로 위에서 ①번과 ④번인데, 이것은 실제로 임의의 함수 P를 정한 다음 계산을 시행해보면 0이 나옴을 알 수 있다.
즉, curl과 gradient 혹은 divergence와 curl은 서로 상쇄관계에 있다고도 해석할 수 있다.

그리고 위의 라플라시안처럼 gradient와 divergence는 서로 비슷하다는 것, 중첩된다는 것을 알수 있다.


마지막으로 ⑤번은 ③번을 이용하여 간단히 나타낼 수 있다.

첫 번째 항은 벡터 함수 P의 curl 두 번이므로 벡터,
두 번째 항은 벡터 함수 P의 div-grad 이므로 벡터,

따라서 마지막 라플라시안은 벡터 함수 P의 벡터 라플라시안임을 알 수 있다.