Min
코안다 효과와 베르누이 원리, 그리고 양력 본문
비행기가 뜨는 원리에 대해 현재 가장 많은 초/중/고 교육과정에서 설명하고 있는 방식은 다음과 같다.
베르누이의 원리에 의하면 유체의 속도가 빨라질수록 압력이 감소한다.
비행기 날개는 위쪽면이 둥근 형태를 띠고 있어 앞쪽에서 위/아래로 갈라진 공기가
뒤에서 동시에 도달하려면 이동경로가 긴 위쪽 공기가 아래쪽보다 훨씬 더 빠르게 움직여야 한다.
그러므로 속력이 빠른 위쪽 공기는 압력이 감소하여 전체적으로 위쪽방향의 알짜힘인 "양력" 이 발생하게 된다.
그러나, 이러한 설명방식은 사실 틀렸다.
그림 1 - 여러 에어포일 형태
(*에어포일 airfoil = 비행기 날개를 수직으로 자른 단면의 모양)
이는 베르누이의 원리를 잘못 적용한 대표적인 예시중의 하나이다.
실제로 비행기 중에는 라이트 형제의 초창기 복엽기 처럼 날개가 거의 평면(날개의 곡률인 camber가 0인 날개)인 것이나,
그림 1 에서 볼 수 있듯이 아래쪽이 더 긴 경로로 만든 초임계 에어포일, 양쪽이 대칭인 에어포일들도 존재한다.
이러한 날개들에 대해서는 경로차가 존재하지 않거나 오히려 아래쪽 공기가 더 빠르게 도착하므로 설명할 수 없다.
그림 2 - 나비에-스톡스 방정식(Navier-Stokes Equations)
u : 속도
f : 단위부피당 외력
ρ : 밀도
p : 압력
ν : 점성계수(viscosity)
비행기가 유체속을 진행할때 어떤 일들이 생기는지를 알려면 간단한 해결책이 있다.
해당하는 조건들을 넣어 그림2 의 나비에-스톡스 방정식(이하 NS)을 풀어주면 된다.
그러나 .. 사실 풀기야 한다면 좋겠지만,
NS방정식이 100만달러(!)의 상금이 걸린 7대 밀레니엄 문제 중의 하나인 것이 문제이다.
NS방정식은 점탄성이 없는 유체의 행동에 관한 비선형 편미분 방정식으로
현재까지 수학적인 해는 알려져 있지 않다.
점탄성(Viscoelasticity)이란 밀가루물이나 갯벌처럼 액체의 특성인 점성과 고체의 특성인 탄성을 모두 갖고 있는 성질이다.
그림 3 - 점탄성을 띤 대표적인 물질인 밀가루물.
손가락을 천천히 움직이면 흐르는 액체처럼 행동하고(점성), 강한 충격을 주면 단단한 고체처럼 튕겨낸다(탄성)
대학에서 미분방정식을 공부해본 이 라면 비선형(Non-linear) 미분방정식의 공포에 대해 체감이 될 것이다
심지어 그 해가 3차원(혹은 시간 까지 포함한다면 4차원 시공간)에 대해 항상 존재하는지 아닌지에 대해서도 불분명하다.
실제 항공역학에서도 NS방정식으로 얻어진 결과들을 아주 많이 사용하고 있지만,
이는 모두 슈퍼컴퓨터의 해석적인 근사해에 의존하고 있는 상황이다.
마치 고차원 방정식의 해를 구하기 위해 x에 수 많은 값들을 하나하나 넣어가며 얻은
근사적으로 해들을 사용하고 있다고 생각하면 된다.
그런데 그렇게 할 슈퍼컴퓨터가 없다면?
실제로 발로 뛰는 수밖에.
풍동실험을 하면 된다.
그림 4 - 풍동실험 결과로 얻어진 에어포일 주변의 공기의 흐름
(Kraaiennest at wikemedia.org)
위 그림은 풍동실험을 통해 얻어진 평범한 에어포일 주변의 공기 흐름을 시각화한 것이다.
양력의 발생 근본원인은 날개의 받음각(Angle of Attack. 즉 AOA!)과 에어포일의 형태 두 가지로 정리된다.
여기서 받음각이란 유체의 흐름에 대한 날개의 각도를 의미하며 실제 대부분의 비행기들의 몸체가 수평면에 대해 살짝 들려져 있는 형태로 양력을 얻고 있다.
날개의 형태는 이렇게 얻어진 양력을 좀더 보충해 주는 역할을 하며 그림1 에서도 보았듯이 다양한 형태의 에어포일들이 존재한다.
받음각이 존재한다면, 유체는 에어포일에 의해 휘어지면서 흐르게 된다.
(물론, 받음각이 0이어도 에어포일의 "부피" 가 0이 아닌 이상 유체는 반드시 휘어지게 된다. 단단한 고체인 에어포일을 관통할 수는 없으니까!)
즉, 결과적으로 이것은 유체가 힘을 받아서 운동상태가 변했다는 것이다.
누구로부터 힘을 받았을까?
바로 날개, 즉 "에어포일" 이다.
그림 5 - 눈에 보이지 않는 공기의 흐름을 관찰하기 위해 주로 연기를 피워서 데이터를 얻는다.
(http://amasci.com/wing/airgif2.html)
그림4 를 보면, 위쪽 에어포일에서 공기는 날개를 따라 아래쪽으로 꺾이면서 흐른다.
이것은 에어포일로 부터 아래쪽으로 당겨지는 힘을 받는 것이다.
혹은 일종의 구심력을 받아 공기가 시계방향으로 "원운동의 일부" 를 하고 있는 것이라 말할 수도 있다.
이것에 대한 반작용으로 에어포일에는 위쪽으로 밀려올라가는 힘이 발생한다.
반대로 아래쪽 에어포일도 살펴보면, 이번에도 공기는 날개를 따라 시계방향으로 원운동을 한다.
마찬가지로 구심력은 아래방향이며, 따라서 반작용으로 아래쪽 에어포일도 위로 밀려올라가는 힘을 "공기로부터" 받는다.
날개 위 아래 작용하는 위쪽으로 밀려올라가는 이 힘, 이것이 바로 양력의 근본이라고 할 수 있겠다.
그림 6 - 설거지 할때 다들 한번씩 해본 경험
대표적인 코안다 효과의 잘못된 예시이다.
공기가 날개 표면을 따라 흘러가는 현상을 가지고 코안다 효과(Coanda effect)로 설명하는 방식이 있는데,
이는 틀린 설명이다.
코안다 효과는 좁고 빠른 "제트(Jet)" 의 흐름에서 제트가 단단하고 휘어진 고체 표면을 따라 흐른다는 것이다.
일반적인 비행기 날개 주변은 제트의 흐름이 아니라 규모가 크고 밀도가 균일한 "층류(Laminar flow)" 이기 때문에 적절한 설명 방식이 아니다.
비슷한 예로 그림6 처럼 숟가락 표면을 따라 졸졸졸 흐르는 물줄기도 흔히 들어지는 코안다 효과의 대표적인 잘못된 예시이다.
코안다 효과의 영향이라기 보다는 물의 표면장력 때문에 발생하는 부착력으로 물 분자가 수저 표면에 달라붙는 것이다.
이것은 유체의 속력이 빠를수록 강하게 달라붙는 코안다 효과와는 달리,
물줄기를 점점 세게 할 수록 부착력이 감소하면서 오히려 숟가락 표면에서 떨어져나가는 모습에서도 표면장력의 기여도를 관찰할 수 있다.
코안다 효과를 재현하려면?
"제트" 를 만들어주면 된다.
바로 아래 그림처럼 물을 아주 세차게 뿜어내면 된다!
그림 7 - 아주 "바람직한" 코안다 효과의 예시. (en.wikipedia.org/wiki/Coandă_effect)
코안다 효과의 결과로 물은 공 표면을 따라 반시계 방향으로 원운동을 하며(구심력은 오른쪽),
따라서 반작용으로 왼쪽 방향으로 물체가 끌려가려는 힘이 발생한다. 이 힘 또한 일종의 양력이다.
(그 힘을 관찰할 수 있도록 실을 열심히 움직이고 있는 우리의 실험자의 모습이다)
가만, 그런데 반작용으로 유체가 반대의 힘을 물체에 준다고?
아까 양력의 원리와 비슷한것 같은데.... 라는 생각이 들었다면 지금까지 잘 이해하면서 읽은 것이다.
정답이다. 이러한 코안다 효과의 결과는 물체 표면에 유체의 흐름을 더 강하게 압착시키는 결과를 가져온다.
즉, 유체는 "더 강력한 구심력" 으로 날개 표면에 달라붙어 흐르게 되고,
이것은 그만큼의 반작용인 "더 강력한 양력" 을 얻을 수 있게 되는 셈이다.
또한 이렇게 코안다 효과로 얻게되는 추가적인 양력은 꽤 강력하다.
그림4 에서도 위쪽 에어포일을 자세히 보면, 앞쪽 공기는 날개에 비교적 근접해서 달라붙는데,
뒤쪽 공기는 앞쪽보다 좀더 에어포일로부터 떨어져 나가있는 모습을 볼 수 있다.
코안다 효과가 발생한다면?
공기가 훨씬 더 날개에 달라붙게 될 것이다!
그림 8 - 코안다 효과를 체험해볼 수 있는 실험.
(좌)둥근 병 위쪽에서 빨대로 바람을 불면 병 바로 아래쪽 수면부터 바람이 퍼진다거나,
(우)종이가 떠오르게 된다.
그림8 처럼 종이 앞쪽을 들고 윗면을 따라 바람을 세차게 불어주면, 아래로 쳐져 있던 종이가 위로 뜨는 것을 볼 수 있다.
그림 9 - 헤어드라이기 위의 탁구공.
주위를 휘감는 제트로 인해 탁구공은 거의 모든 방향(주로 공 중심에서 바깥쪽 방향)으로
코안다 효과로 인한 반작용 힘을 받는다. 따라서 알짜힘이 거의 0이 되어 공중에 떠 있게 된다.
실제로 항공기 중에는 이러한 코안다 효과를 이용하여 뿜어내는 제트의 일부를 날개 앞쪽에서 분사함으로써
강력한 양력을 얻도록 설계된 항공기들도 존재한다.
즉, 앞에서 설명한 "추가적인 양력" 을 잘 활용하는 것이다.
이것은 항공기가 더 느린 유체 속에서도(즉, 항공기 자체가 더 느린 속도일지라도) 날 수 있을만큼
충분한 양력을 얻을 수 있도록 하는 아주 똑똑하고도 강력한 방식인 것이다.
그림 10 - 코안다 효과로 추가적인 양력을 얻는 대표적인 기종인 AN-74
제트 분사구가 날개 바로 앞에 달려있어 위쪽 날개로 제트를 뿜어낼 수 있다.
과거 라이트 형제가 비행기를 개발할 당시에는 항공 유체역학에 대한 지식이 전무했다.
이 시대에는 얇고 가벼운 날개가 훨씬 비행에 유리할 것이라는 것이 정설이자 유행(?)이었다.
라이트 형제 또한 이러한 유행에서 자유롭지 못했다.
그리하여 실제 비행에서 발생하는 난류의 요동에 대해 불안정하게 떨리는 얇은 날개를 버텨주기 위해
날개 두 개를 연결한 복엽기 형태가 안정적이라는 경험적인 사실을 수많은 시행착오를 거쳐 얻게 된 것이다.
현대의 인류도 슈퍼컴퓨터라는 좋은 도구만 추가되었을 뿐, 사실 라이트 형제가 했던 시대와 크게 달라지지 않았다.
강력한 최종보스인 NS방정식이 버티고 있는 이상,
그 누구도 컴퓨팅 시뮬레이션이나 라이트 형제의 시행착오(풍동실험)로부터 자유롭지 못하다.
초음속 비행기의 뾰족한 날개 형태가 대표적인 사례가 되겠다.
1968년 나사의 Whitcomb은 초음속 비행을 위한 날개를 연구하다가
수학적인 결론이 아닌 "직관" 을 바탕으로 비행기 전단을 뾰족하게 만드는 형태를 떠올렸다.
이를 바탕으로 날개를 설계한 후 랭리의 풍동터널에서 수많은 테스트를 거쳐
현대의 초음속 비행기의 에어포일인 초임계 에어포일(Supercritical Airfoil)형태를 정립해낸 것이다.
(기억이 안나는 이는 맨 위의 그림1 을 참고하라)
이것은 기존의 양력 발생원리와 무관하게, 초음속 비행에서 발생하는 충격파를 견디기 위한 것으로
앞단의 표면적을 최소화한 형태이다.
오히려 초음속이 아닌 저속비행에서는 충분한 양력을 얻지 못하는,
엄청나게 빠른 유체의 흐름에 적응하는 기존과는 다른 새로운 형태의 에어포일을 인류는 발견해낸 것이다.
시작은 직관이었으나 수많은 테스트를 통한 "제련" 끝에.
그림 11 - 초음속 비행중인 날개 주변의 충격파를 찍은 사진(좌)과 시뮬레이션 결과(우) (NASA)
NS방정식의 수학적 해가 풀리지 않는 이상,
우리는 에어포일 주변의 공기의 흐름을 100% 정확하게 예측하거나 계산할 수 없다.
실제로 날개 형태를 만들어 풍동터널에 집어넣고 테스트를 해봐야 한다.
변화무쌍한 난류(Turbulence)도 NS방정식이 낳은 괴물같은 자식 중의 하나에 불과하다.
그 유명한 리처드 파인만은 "난류야 말로 인류가 해결해야 할 최대의 난제" 라고 하였다.
이는 나비에-스톡스 방정식의 완전한 수학적 해를 구하는 것과도 같은 말이 되며 이루어진다면
일기예보의 100% 정확도, 비행기나 자동차 구조의 비약적인 발전,
이 외에 예상하기 힘든 수 많은 문제들도 함께 해결되어 인류의 또 다른 특이점(Singularity)이 되는 시기일 것이다.
'Daily > Major' 카테고리의 다른 글
| 빗면과 사이클로이드에서 마찰력에 의해 손실된 에너지는 같은가? (11) | 2019.09.13 |
|---|---|
| 전향력, 코리올리 효과(Coriolis Effect), 관성력 (5) | 2018.05.06 |
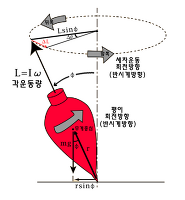
| 팽이와 지구 세차운동의 차이 (8) | 2017.11.19 |
| 원소주기율표 (1) | 2017.05.29 |
| LIGO의 중력파 검출에 관한 이야기 (1) | 2016.02.12 |