Min
빗면과 사이클로이드에서 마찰력에 의해 손실된 에너지는 같은가? 본문
첫 시작은 어떤 학생의 실험 결과를 보는 도중이었다.
실험 아이디어는 교과서에도 자주 등장하는 간단한 실험이다.
같은 높이의 사이클로이드 트랙과 빗면 트랙을 제작한 후 동일한 물체를 최고점에서 가만히 놓는다.
최저점에 동일한 나무도막을 놓고 물체가 나무도막과 함께 미끄러지다가 정지한 거리를 측정한다.

두 물체가 함께 이동하면서 멈춘 거리를 비교하면 충돌 직전 질량 \(m\)인 물체의 운동에너지를 비교할 수 있다.
즉, 에너지 보존 측면에서 다음과 같다.
처음 질량 \(m\)인 물체의 위치에너지(\(E_1\)) = 트랙을 따라 내려오며 마찰력으로 손실된 에너지(\(E_2\)) + 충돌 직전의 운동에너지(\(E_3\))
또한, 충돌 직전의 운동에너지(\(E_3\)) = 비탄성 충돌과정에서 손실된 에너지(\(E_4\)) + 충돌 후 \(m\)과 \(M\)의 운동에너지(\(E_5\))이고,
충돌 후 \(m\)과 \(M\)의 운동에너지(\(E_6\)) = 두 물체와 바닥사이의 마찰력(\(f'\)) \(\times\) \(m\)과 \(M\)이 함께 이동한 거리(\(d\)) 로 정리된다.
\(E_3\)~\(E_6\), 그리고 \(f'd\)까지는 아무런 문제가 없는데 문제는 \(E_2\)이다.
"사이클로이드 트랙과 단순 직선의 빗면 트랙에서 마찰력에 의해 손실되는 에너지(\(E_2\))가 같은가?"
얼핏 단순해보이는 질문일 수 있으나 물리적인 직관으로 해결하기가 쉽지는 않아 보인다.
일단, 트랙을 따라 내려오며 마찰력으로 손실된 에너지 \(E_2\)는 트랙에서의 마찰력(\(f\)) \(\times\)트랙의 길이(\(s\))이다.
빗면에서는 \(f\), \(s\) 두 값이 모두 상수이지만 사이클로이드에서는 각 지점마다 모두 변한다.
결국 미분을 통해 \(f ds\)을 끌어낸 후, \(s\)에 대하여 적분을 해줘야 하는 것이다.
그래서 사이클로이드 방정식을 끌고와서 \(ds\)를 구하면 구할 수 있겠네~ 하는 생각이 들어 구해보았다.
1. 빗면에서 마찰력이 한 일

굉장히 심플하다. 고등 물리Ⅰ 고전역학 파트에서 자주 등장하는 예제.
핵심은 물체의 무게인 \(mg\)를 빗면에 수평인 성분과 수직인 성분으로 분해하는 것.
여기서 수평인 성분 \(mg \sin\theta\)는 물체를 빗면 아래로 끌어내리는 힘이고,
수직인 성분 \(mg \cos\theta\)는 빗면에서 작용하는 수직항력으로 운동마찰계수 \(\mu\)를 곱하여 마찰력 \(\mu mg \cos\theta\)...①를 만든다.
빗면 높이가 \(h\)일 때 빗면의 길이는 \(\displaystyle \frac{h}{\sin\theta}\)...② 이므로 마찰력이 한 일은 ①과 ②를 곱하면 된다.
$$\therefore \mu mgh\cdot\frac{\cos\theta}{\sin\theta}=\mu mgh\cot\theta $$
2. 사이클로이드에서 마찰력이 한 일
앞서 언급했듯이 다소 복잡하다. 면 위에서의 \(\theta\)가 계속 바뀌기 때문에 마찰력 또한 바뀌게 된다.
일단 사이클로이드의 매개변수 방정식은 다음과 같다.
$$x=r(\theta -\sin\theta )$$
$$y=r(1-\cos\theta )$$
사이클로이드 그래프는 다음과 같이 \(\theta\), \(r\)에 따라 계속 반복된다.
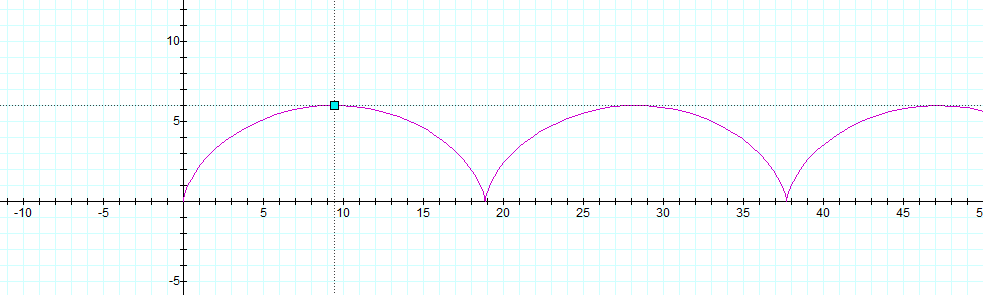
여기서 그래프의 딱 절반위치, 즉 사이클로이드 곡선에서 최고 높이인 \((\pi r,2r)\)인 점 까지의 사이클로이드를 이용하여 우리의 물체 낙하 실험에 사용한다고 가정해보자.(\(\theta = \pi, r=r\)일 때)
(안 그러면 내려오던 물체가 다시 오르막길을 가버린다.)
이렇게 되면 위에서 계산했던 빗면의 가로, 세로가 고정되어 버린다.
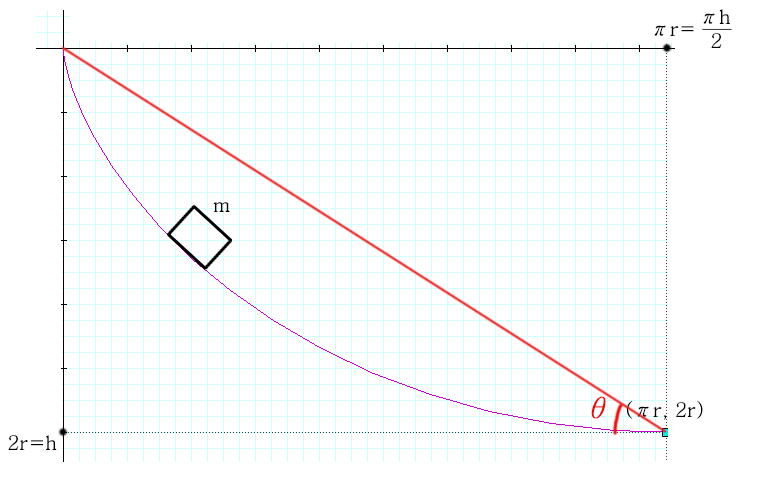
빗면 가로 길이는 \(\displaystyle \frac{\pi h}{2}\), 높이는 \(h\)이므로 \(\cot\theta = \displaystyle \frac{\pi}{2}\)가 된다.
따라서 우리가 처음 구했던 빗면에서의 마찰력이 한 일은 \(\displaystyle \frac{\pi}{2} \mu mgh\)로 조금 더 정리된다.
다시 사이클로이드로 돌아가보면, 사이클로이드 위의 한 점 \((x, y)\)위에 있는 물체는 기울기가 \(\displaystyle \frac{dy}{dx}\) 인 직선과 접한다.
또한 이 직선이 \(x\)축과 이루는 각을 \(\alpha\)라고 하면, 빗면에서와 마찬가지 방법으로 \(mg\)의 면에 대한 수직성분인 \(mg\cos\alpha\)에서 \(\alpha\)에 대한 마찰력 함수 \(f(\alpha ) = \mu mg\cos\alpha\)라고 적을 수 있다.
+(21.3.19 추가) 그러나 직선이 아닌 휘어진 트랙을 움직이는 물체는 구심력의 영향도 추가로 받게 된다.
간단히 생각하면 곡률반지름 \(R\)에 대하여 \(\displaystyle \frac{mv^2}{R}\) 만큼의 원심력으로 인해 트랙에 대하여 수직으로 내리누르는 힘이 추가된다고 생각하면 된다.
결국 마찰력은 중력의 수직성분 + 원심력 으로 간주 할 수 있으므로 다음과 같이 합쳐진 형태가 된다.
$$f(\alpha ) = \mu \left( mg\cos\alpha + \frac{mv^2}{R} \right) $$
1)중력의 수직성분 구하기
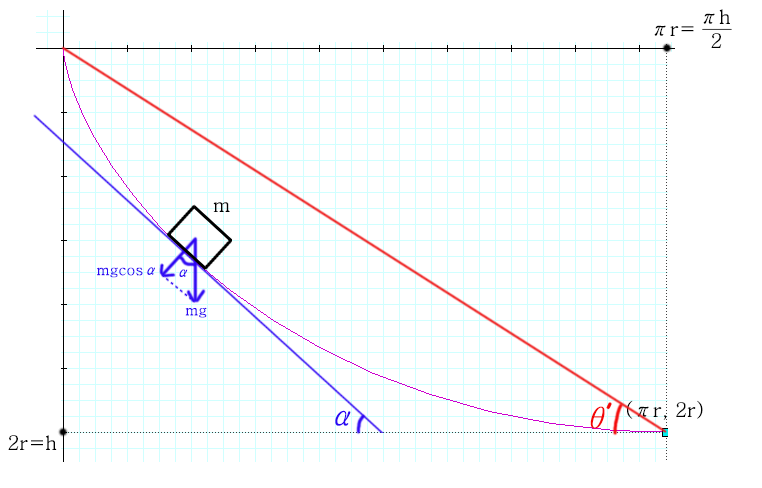
매개변수 미분을 이용하여 기울기를 구해주면,
\(\displaystyle \frac{dy}{dx} = \frac{\frac{dy}{d\theta }}{\frac{dx}{d\theta }} = \frac{r(sin\theta )}{r(1-cos\theta )}\) 이다.
간단히 하기 위해 약간의 트릭을 사용하면 \(\displaystyle \frac{1-cos\theta }{2} = sin^2 \frac{\theta }{2}\) 에서 \(\displaystyle \frac{2}{1-cos\theta } = \frac{1}{sin^2 \frac{\theta }{2}}\)이다.
\(\displaystyle sin\theta = 2sin\frac{\theta }{2} cos\frac{\theta }{2}\)이므로 대입해주면
\(\displaystyle \frac{r(sin\theta )}{r(1-cos\theta )} = cot\frac{\theta }{2}\) 으로 간단히 된다.
즉, 기울기인 \(\displaystyle \frac{dy}{dx}= tan\alpha = cot\frac{\theta }{2}\)가 되는 것.(단, \(\theta\)의 범위는 \(0\sim~\pi \))
우리가 궁금한 것은 \(cos\alpha\)이므로 정리해보면,
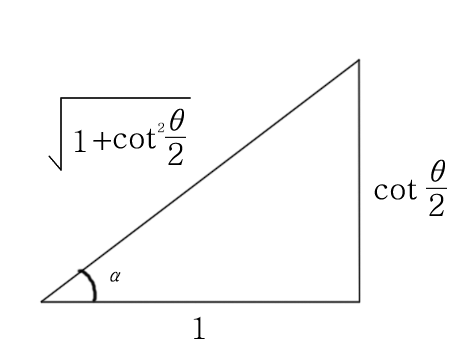
\(\displaystyle mgcos\alpha= mg\frac{1}{\sqrt{1+cot^2 \frac{\theta}{2}}} = mgsin\frac{\theta}{2}\) 가 된다.........③
2)원심력 구하기
곡면일 경우 아주 미소한 영역에서 접하는 원을 그려 곡률반지름을 구할 수 있다. 기본적인 원의 성질에서 중심각의 크기가 \(\phi\), 호의 길이가 \(l\)이라면 반지름 \(R=l\phi \)인데, \(\phi\)가 아주 미소한 경우는 다음과 같이 나타낼 수 있다.
$$ R = \bigl\vert \frac{dl}{d\phi } \bigr\vert$$
\(x=f(t), y=f(t)\)로 표현된 매개변수 함수의 경우 곡률반경은 다음과 같다.
$$ R = \frac{(x'^2 + y'^2)^{\frac{3}{2}}}{|x'y'' - y'x''|}$$
이제 사이클로이드 함수를 넣어 계산을 해보면 다음과 같다.(\(\displaystyle x' = \frac{dx}{d\theta }\))
$$ R = \frac{(r^2(cos^2 \theta - 2cos\theta + 1 + sin^2\theta ))^{\frac{3}{2}}}{|r^2(cos\theta - cos^2 \theta - sin^2 \theta |} = \frac{(4r^2 sin^2 \frac{\theta }{2})^{\frac{3}{2}}}{2r^2 sin^2 \frac{\theta }{2}} = 4rsin \frac{\theta}{2} $$
따라서 원심력 = \(\displaystyle \frac{mv^2}{4r sin\frac{\theta}{2}} \) 이 된다..........④
③과 ④를 더한 값이 사이클로이드의 한 지점에서의 면을 수직으로 내리 누르는 힘이 되며, 따라서 여기에 마찰계수 \(\mu\)를 곱한 만큼이 순간의 마찰력이 되겠다.
④에서 문제점은 \(v\)를 나타내어야한다는 점인데, 벡터임을 생각해보면 \(v_x\) 와 \(v_y\)로 나누어 생각할 수 있고, 각각의 성분은 \(x, y\)를 시간 \(t\)로 미분한 것이다.
예를 들면 \(\displaystyle v_x = \frac{dx}{dt} = \frac{dx}{d\theta}\cdot \frac{d\theta}{dt} \) 인 셈.
벡터합을 생각해보면 결국 \(\displaystyle |\vec{v}| = \sqrt{x'^2+y'^2}\)이 됨을 알 수 있다.
그러므로 중력의 수직 성분(③)과 원심력을 합한 마찰력 F는 다음과 같다.
$$ F(\theta ) = \mu mgsin\frac{\theta}{2} + \mu mr\omega^2 sin \frac{\theta}{2}$$
(여기서 \(\displaystyle \omega = \frac{d\theta}{dt} \) )
3)마찰력에 의해 손실된 에너지 구하기
아주 미소한 길이 \(dl\) 동안 이 마찰력에 의해 에너지가 손실되는 것이다.
그러니 사이클로이드의 길이 함수를 구해야 한다.
매개변수로 표현된 함수에 대해서 길이 \(l(\theta )= \displaystyle \int \sqrt{\left({\frac{dx}{d\theta }}\right)^2+\left(\frac{dy}{d\theta }\right) ^2} d\theta \)로 구해진다.
사이클로이드의 \(x, y\)식을 넣어 정리하면
$$\displaystyle \int \sqrt{r^2 (cos^2 \theta - 2cos\theta + 1 + sin^2 \theta )} d\theta $$
$$\displaystyle = r \int \sqrt{2(1-cos\theta )} d\theta $$
$$\displaystyle = r \int \sqrt{4sin^2 \frac{\theta }{2}} d\theta $$
$$\displaystyle = 2r \int sin\frac{\theta }{2} d\theta $$ (\(\because \) 주어진 범위에서 \(\displaystyle sin \frac{\theta }{2}\)는 항상 양수)
따라서 \(\displaystyle dl = 2rsin\frac{\theta }{2} d\theta \)이므로 마찰력에 의해 손실된 미소에너지 \(dE\)는 다음과 같다.
$$ dE = F(\theta )\cdot dl = 2\mu rmg sin^2 \frac{\theta }{2} \cdot d\theta + 2\mu mr^2 sin^2 \frac{\theta }{2}\cdot (\frac{d\theta }{dt})^2 \cdot d\theta $$
이 식을 \(\theta = 0 \sim \pi\)까지 정적분해주면 원하는 값이 구해지겠다.
앞부분 적분은 쉽게 구할 수 있다.
$$ E = \mu mgh \int_{0}^{\pi } \frac{1-cos\theta }{2} d\theta $$
$$ = \frac{1}{2} \mu mgh \left[\theta - sin\theta \right]_{0}^{\pi } $$
$$ = \frac{\pi }{2} \mu mgh $$
이 값은 빗면에서 구했던 마찰력에 의해 손실된 에너지 값과 동일하다.
뒷부분 적분은 상당히 복잡해 보인다.. (풀다가 막힘 ㄷㄷ)
지금 당장 확실한 점은 뒷부분 텀이 추가로 있으므로,
빗면에서 마찰력에 의해 손실된 에너지 \(<\) 사이클로이드에서 마찰력에 의해 손실된 에너지
라는 점 이다.
(단, 이 때 사이클로이드는 절반 만큼의 트랙이며, 빗면은 이 사이클로이드의 시작점과 끝점을 이은 빗면을 의미한다)
**하지만 실제상황에서는 그렇듯 오차가 발생한다.
일단 마찰력 공식인 \(f= \mu N\)부터가 물리적인 근사식일 뿐더러 이상적인 사이클로이드 곡선 제작은 3D프린터가 있지 않는 이상 현실적으로 만들기가 상당히 어렵다.
게다가 물체가 미끄러져 내려오면서 항상 표면에 완벽하게 닿아있다고 가정하기도 어렵다.
이런 여러가지 이유들 때문에 실험한 학생의 데이터에서는 사이클로이드 곡선을 내려온 물체가 마찰력에 의해 에너지를 오히려 덜 잃어버린 결과값들이 나왔나보다.
'Daily > Major' 카테고리의 다른 글
| [일천물] 3. 양자역학 - a (2) | 2021.01.31 |
|---|---|
| 생물포스터 제작 완료 (2) | 2021.01.13 |
| 전향력, 코리올리 효과(Coriolis Effect), 관성력 (5) | 2018.05.06 |
| 코안다 효과와 베르누이 원리, 그리고 양력 (66) | 2018.02.12 |
| 팽이와 지구 세차운동의 차이 (8) | 2017.11.19 |




