Min
[일천물] 3. 양자역학 - a 본문
양자역학.
아마 평범한 사람들에겐 굉장히 많이 들어 익숙하면서도, 실제로 설명하기엔 망설여지고,
그러면서 뭔가 있어보이는 과학(?)을 나타내는 단어로 많이 사용되는 말일 것이다.
직업이 어떻게 되세요?
과학자입니다.
오~ 무슨 연구하세요?
양자역학입니다.
..아하....
이런 느낌이랄까.
예를 들면, 스타크래프트1 의 광양자 캐논 이라던가,
(Photon Cannon. 다만 Photon은 사실 '광자' 가 맞는 번역이다.
지금은 광자포 라고 수정되었지만, 최초 번역가는 뭔가 더 있어보이도록 '광양자' 로 번역하지 않았을까..?)
미드 프린지(Fringe)의 시작화면에 나오는 여러 단어들 중에도 이 '양자' 가 나온다.

비주류과학(Fringe Science)과 관련이 있거나 원론적인 단어들이 등장한다.
양자얽힘(Quantum Entanglement), 철학자의 돌(Philosopher's Stone), 사이코메트리(Psychometry) 등이 눈에 띤다. 그야말로 '있어보이는' 단어들의 향연이다.
이렇게 적고 보니 굉장히 거창한 것 같은데, 양자역학이 무엇인가- 에 대한 질문에는
다음과 같이 대답할 수 있겠다.
양자역학이란,
양자(Quantum)들의 특성, 성질들에 대한 학문이다.
....
적고보니 너무나 당연한 이야기......
그러나 아직 돌을 던지기에는 이르다!
그렇다면 오늘의 주인공, 양자란 무엇인가?
이것을 설명하기에 앞서 잠시 19세기 중반까지의 과학자들의 생각을 알아볼 필요가 있다.
이때까지의 과학은 뉴턴의 고전역학이 얼마나 굉장한지, 찬양하는 시기라고 해도 과언이 아니다.
그때까지의 모든 실험들은 고전역학에 의해(물론 그 당시에는 '고전' 이라고 부르지 않았겠지만!)
설명이 가능하고, 예측또한 가능했다.
이를테면,
행성들의 위치를 관측, 계산하여 행성들이 일렬로 늘어서는
행성 정렬(Planet align)이 일어나는 시기를 정확히 예측한다거나 하는 식이다.

과학자1 : 야야, 얘들아 내가 계산해보니까 3년 뒤 오늘 3시에 수금지화목토 전부 일렬정렬이더라?
과학자들 : 올ㅋ 계산좀했네.
과학자2 : 나나나나 나도!! 난 월식 계산했어!! 정확히 13년 4개월 2일 후야!!
과학자들 : 캬~ 고생했다. 오늘도 우리들에게 연구할 양식을 주신 뉴턴 센-세에게 묵념.
그러나, 여기에 처음으로 난관이 닥치게 된다.
19세기 후반 즈음부터 시작된 전자, 양성자, 중성자 등의 아주 작은 입자(소립자)에 관한 실험과
빛에 관한 실험들이 진행되면서부터이다.
그 전까지는 잘만 적용되던 뉴턴의 고전역학이 소립자들에 대해서는 적용이 안되었던 것이다.
이 입자들이 대체 속도가 얼마인지, 위치가 어디인지 종잡을수가 없었다.
특히나 빛!
빛에 대해서는 당시의 과학자들이 기존까지 쌓아왔던 뉴턴 센-세의 고전역학이 거의 통하지 않았다!
저번 특수상대론에서도 그러더니... '하... 또 빛 너냐?' 라는 생각이 들 수 밖에!
그때까지 하늘의 천체들의 위치를 계산하여 '예언' 하던 과학자들이,
발밑의 아주 작은 입자들에 대해서는 갑자기 눈뜬 장님이 되어버린 것이다!
따라서 기존의 뉴턴역학으로는 설명히 불가능한, 소립자들의 행동방식을 설명하는 것으로
양자론(Quantum theory)이 제기되기에 이르렀다.
여태까지 가지고 있던 곡괭이로는 캘 수가 없는 광맥을 발견했다면,
새로운 곡괭이를 개발해야하는 것이 인지상정!
이때, 새로운 곡괭이를 만드는 사람들은 크게 두 학파로 나뉘게 된다.
첫번째는 보어, 하이젠베르크 등등의 "입자좋아파"
두번째는 드브로이, 슈뢰딩거 등등의 "파동이최고파".
처음에는 서로 내꺼가 저 광석 캐기에 가장 적당하다, 헛소리 니 곡괭이로는 콧구멍도 못파겠다,
말다했냐 그래 내껄로 니 콧구멍 파줄게-
라며 지지고 볶고 싸우던 두 파벌이었지만,
후에 이르러서는, 두 곡괭이, 아니 두 가지 관점이 동일하다는 것이 증명되었다.
? 잠깐, 이 말이 의미하는 바는?
그렇다. 입자와 파동은 완벽히 같다는 것이다!

갑자기 낯선사람이 나타나서 '난 사실 너의 쌍둥이 동생이야' 라고 하면 얼마나 황당할까?
심지어 척보기에 그 낯선사람은 나와 전혀 닮지도 않았는데!
당시의 과학자들이 느꼈던 심정도 비슷했으리라.
빛이 입자냐 파동이냐 - 에 관한 논쟁은 엄청난 전쟁이었다.
재미있는점은, 이 주장 또한 시대적 흐름을 타서
초반에는 빛이 파동이라는 주장이 대세였으나,
아인슈타인 갓-센세께서 광전효과(Photoelectric effect)로
그 유명한 노벨상을 받아버리는 바람에 홀라당 뒤집어졌다.
여기에 대한 후문으로 사실 상대성이론이 훨씬 더 유명한 연구였지만,
당시의 노벨상위원회는 뚜렷하게 현실에 드러나고 구체적인 연구결과에만 상을 주는 경향이 있었다.
그 대-단한 아인슈타인에게 노벨상을 주긴 줘야할텐데,
이놈의 상대성이론이라는게 별로 쓸모도 없고(그때까지는) 공상과학과도 같은 이야기라
하는 수 없이 작은 논문중에 고르고 고른 것이 광전효과라는 후문이 있다.
광전효과는 간단히 말하면 빛 가지고 구슬치기 하는 실험으로,
빛의 입자적인 모습을 증명하는 현상이 되겠다.
출렁거리는 물결파는 한 덩어리인 '구슬' 이 아니니깐!
아인슈타인 센-세의 지원군에 힘입어 다시 빛의 입자론이 강력하게 힘을 받기 시작하는 등,
수 십년동안 서로 엎치락 뒤치락 하다가
이 모든 사태를 한 마디로 정리해버린 사나이가 나타났다.
1927년, 베르너 하이젠베르크는 "불확정성의 원리" 를 발표하면서
"빛은 입자, 파동 그 무엇도 아니다." 라고 이야기한다.

"응~ 입자파 파동파 너네 다 틀림~"
여기서 또 재미있는 일화가 있는데,
하이젠베르크는 불확정성의 원리를 발표한 논문 끝부분에
"어.. 음.. 그리고 마지막으로 솔직하게 말하는건데, 내가 이 이론들 만드는 데에는
아인슈타인의 상대성원리가 조금.. 아니 꽤 많이 도움이 되었다."
라고 언급하며 아인슈타인에게 감사를 표한다.
그러나 얄궂게도 아인슈타인 본인은 불확정성의 원리를 매~우 싫어했다.
아인슈타인의 유명한 "신은 주사위 놀이따위 하지 않는다고!!!" 라는 발언도 그런 생각에서 나온 말이다.
불확정성의 원리는 굉장히 다양한 말로 표현이 가능한데,
이중성(Duality)에 관해서는 다음과 같다.
"어떤 물질의 입자적 특성과 파동적 특성을 동시에 측정하는 것은 불가능하다."
이게 무슨말인지 생각해보기 전에, 입자적 특성과 파동적 특성에 대해 고민을 해보자.
입자적 특성에는 어떤 것이 있을까?
눈앞의 아무 물건을 집어들고 특징들을 찾아보자.
두 가지 장소에 동시에 존재할 수 없다!
일정한 크기를 가진다!
손으로 만질 수 있다!
등등.
반면, 파동적 특성이란?
그림 3 에서의 물결파나 눈에 보이지는 않지만 우리 주변에 떠다니는 와이파이 신호를 상상하면 된다.
여러 방향으로 퍼진다거나, 손으로 만질 수 없다거나, 일정한 크기가 없다거나.
"아니 이봐여.. 근데 볼링공이랑 와이파이 신호는 당연히 다르잖아여..
와이파이에서 볼링공의 특징을 측정할 수 없다 - 라는 말은 당연한 말 아니냐구욧!!"
충분히 당연한 지적이다.
그런 당신에게 추천하는 한 상품!.. 이 아니라, 여기 모의 실험 하나를 소개한다!
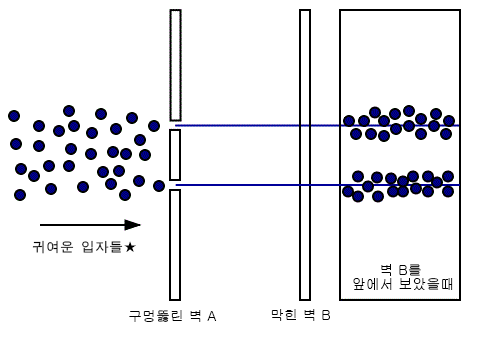
왼쪽에서 귀여운 파랑 구슬들을 쏘아보낸다고 생각해보자.
우리의 이 카와이★ 한 구슬은 매우 단단해서 절대로 쪼개지지 않는다.
그리고 물론 구슬들은 의심의 여지 없이 입자이다.
또한 이 구슬들은 벽을 관통할 수는 없으므로,
막힌 벽으로 날아간다면 더 이상 진행하지 못하고 그 자리에서 멈추거나 반대로 튕겨나올 것이다.
우리의 앞에는 벽이 2개(A, B) 있는데,
벽 A에는 구슬 한두개가 지나갈만한 작은 구멍이 두 개 뚫려있다.
그럼 벽 B의 어떠한 곳들에 구슬들이 많이 도달할까?
큰 어려움 없이 그림 5 처럼, 벽 A의 구멍 부근에 해당되는 곳에서
구슬들이 가장 많이 도착할 것이라고 예상할 수 있을 것이다.
좀 낮은 확률이지만 구멍에서 조금 벗어난 곳에도 구슬이 도착할 수 있겠지만,
대부분은 구멍 주변에 몰려있을 것이다.
그리고 결코! 이 구슬은 날아가다가 갑자기 반으로 쪼개져 A의 두 구멍을 각각 지나간다거나,
한 구멍 들어갔다가 다시 지혼자 되돌아와서 다른 구멍으로 나온다거나,
하는 일들은 벌어지지 않는다.
이것이 바로 입자의 대표적인 특징이 되겠다.
그러면 파동으로 같은 실험을 하면 어떻게 될까?
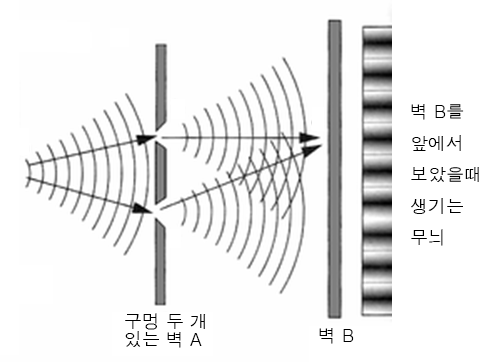
그림 5 의 상황과는 사뭇 다른 모습이 보인다.
무늬가 밝을 수록 많이 도달한 것이고, 어두운 부분은 적게 도달한 것이다.
귀엽지는 않지만, 나름대로 매력있는 파동을 데리고 같은 실험을 해보았다.
역시나 우리의 짱짱튼튼한 벽은 파동도 막아내기때문에 구멍으로만 파동이 진행할 수 있다.
그런데, 입자로 실험했을때와는 사뭇 다른 결과가 눈에 띤다.
일단, 파동은 한 덩어리 덩어리로 구별되지도 않는데다가,
입자처럼 구멍 주변에서만 관찰되지도 않는다.
많이 도달한 부분과 적게 도달한 부분이 일정한 패턴처럼 나타난 것이다!
이것이 바로 파동의 대표적인 특징 중의 하나인 "간섭무늬" 가 되겠다.
입자와는 달리 오지랖이 엄청난 파동은,
옆의 구멍에서 나온 다른 파동과 서로 지지고 볶고 하면서 간섭을 하기 때문에
저런 요상한 무늬가 나타나게 된다.
자, 이것이 대표적인 입자와 파동을 구분짓는 특징이다.
이 멋-진 입자파동 판별장치를 이용하여 궁금한 물체는 이 실험을 해보면
입자인지 파동인지 명확하게 결과가 나오게 된다!
입자면 간섭무늬가 없을 것이고, 파동이면 간섭무늬가 있을 것이다.
얼마나 명쾌한 결론인가!
그런데! 자연의 취미가 과학자 괴롭히기라는 말 처럼,
일련의 과학자들이 아주 작은 입자인 "전자(Electron)" 를 가지고 한 똑같은 실험에서
예상과는 다른 엄청난 결과가 발생하게 된다!
*21.1.31.
왜인지는 모르겠지만 그림들이 다 깨져서 수정하였습니다.
(+덤으로 내용 표현도 수정!)
'Daily > Major' 카테고리의 다른 글
| [일천물] - 3. 양자역학 - c(수정) (3) | 2021.01.31 |
|---|---|
| [일천물] - 3. 양자역학 - b(수정) (2) | 2021.01.31 |
| 생물포스터 제작 완료 (2) | 2021.01.13 |
| 빗면과 사이클로이드에서 마찰력에 의해 손실된 에너지는 같은가? (11) | 2019.09.13 |
| 전향력, 코리올리 효과(Coriolis Effect), 관성력 (5) | 2018.05.06 |