Min
특수상대성이론, 로렌츠변환, 그리고 시공간 본문
원래 지식in 어떤분 질문에 대한 답변을 쓰던건데.. 쓰다보니 너무길고도 자세하게 되버렸다 '' ;;
한마디로 정리하면 오버한 답변, 시험정리 글이 되어 남기노니... 라고나 할까 : )
---------------------------------------------------------------------------
A라는 사람이 점 P의 좌표를 측정하여 (x,y,z) 라는 좌표값을 얻었다고하면,
B라는 사람은 시간 t일때 x축방향으로 v의 속도로 움직이는 좌표계에서 점 P를 측정하여
(x',y',z') 이라는 값을 얻었을텐데, x' = x-vt , y' = y, z' = z 의 관계가 성립합니다.
이것을 갈릴리안 변환(Galilean transformation)이라고 부르며, 직관적으로 이해하기도 쉽고 비교적 정확하게 들어맞는듯 합니다.
이 갈릴리안 변환의 내제된 법칙으로 갈릴레이의 상대성이라는 것이 있는데, 그것은 다음과같은 한문장으로 표현됩니다.
모든 관성계에서 물리법칙은 동일하게 서술된다.
이것은 물리에 내제된 절대적인 법칙으로, 바꿔말하면 다음과 같습니다.
절대적인 좌표계는 존재하지 않는다.(또는, 특정 물체의 절대속도를 측정할수 없다)
두번째문장은 첫번째 문장으로부터 도출되는 결론이며, 반대로 두번째문장이 성립해야만 첫번째 법칙이 맞게됩니다. 필요충분 관계에 있다고 할수 있겠네요.
그 이유를 차근차근 설명해보자면..
일단, 관성계라는것은 외력이 0인 system 입니다.
또한 뉴턴제1법칙에서 보면 알수 있듯이 외부로부터의 힘이 없을경우 물체는 정지하거나 등속(도)운동을 하게되지요.
갈릴레이의 상대성에서 도출되는 파급효과는 엄청납니다. 특수상대성이론도 이것에서부터 출발하는것이죠.
예를들어, 등속운동을 하는 기차에 탄 사람이 공을 연직방향으로 던진다고 생각해봅시다. (이 기차는 등속운동이외의 다른 진동이나 마찰등이 없습니다)
그럼 공은 수직으로 올라갔다가 다시 수직으로 내려오겠죠. 여기서 그사람은 이러한 법칙을 찾을수 있겠죠.
-> 공을 수직으로 던지면 수직으로 떨어진다.
그럼, 정지해있는 땅위에서해도 어떨까요? 똑같은 결과가 나오는것을 알수있습니다. 이렇듯, 만약 기차내부에서 외부를 볼수있는 조건이 없다면, 탑승자는 자신이 등속운동상태인지 정지상태인지 구분을 할 수 없게됩니다. 그러므로 반드시 모든 물리법칙은 동일하게 서술되어야합니다.
만약 물리법칙의 차이가 있다면-예를들어 기차속도가 100m/s가되면 공이 떨어질때 속도의 1/100 하여 1m 뒤로 밀린다거나 하는 식-탑승자는 다른실험결과와의 측정값을 비교하여 자신의 system이 등속운동중인것을 알아냅니다.
즉, 절대속도를 알아내게되는데 갈릴레이 상대성에 의하여 이것은 불가능합니다. 그러므로 관성계에서 모든 물리법칙은 동일하게 서술되어야 하는 것이죠.
19세기 중반까지는 이러한 법칙에 별다른 문제가 없었습니다.
그런데, 맥스웰이 전기와 자기를 통합한 맥스웰방정식을 발표하면서, 빛의 행동양식의 거의 대부분을 밝혀냈는데 여기서 문제가 발생한 것입니다.
맥스웰방정식을 갈릴리안 변환을 하였더니 형태가 달라진 것입니다. 이말은, 등속운동하는 계와, 정지상태의 계에서는 빛에 관한 법칙들이 달라지게 된다는 것입니다. 그러나 알다시피 이것은 절대로 불가능합니다.
만약 가능하다면 이 차이를 측정하여 절대속도를 구할텐데 이것은 불가능하기때문입니다.
따라서 경우는 두가지밖에 없습니다.
1. 맥스웰 방정식이 틀렸거나, 2. 갈릴리안 변환이 틀렸거나.
여러 실험을 거듭한결과 맥스웰방정식은 절대로 맞을수밖에 없는 것으로 판명되었고,
이때 로렌츠에 의하여 수정된 갈릴리안 변환, 즉 로렌츠 변환(Lorentz transformation)이 만들어졌습니다.
로렌츠변환의 전제조건은 모든 관성계에서 광속 c가 동일한 값을 가진다는 것입니다.
즉, 빛에대해서는 상대속도 개념이 통하지 않는 다거나, 나아가서 우리가 알고있는 상대속도에 대한 개념이 틀렸다는 것을 의미합니다.
이 사실은 맥스웰방정식이 기본적으로 내포하고있는 사실로써, 맥스웰방정식이 참이라는 것이 판명되어 기존의 갈릴리안 변환에 로렌츠가 광속 c가 불변한다는 조건을 추가하여 새롭게 만들어 내었습니다.
여기에 추가적으로 속도 v가 매우느리다면, 우리가알고있는 갈릴리안 변환의 형태가 되도록 하는 꼴을 찾은 결과로 탄생된 로렌츠 변환식은 다음과 같이 나타내어집니다.
x' = γ(x-vt)
y' = y
z' = z
t' = γ(t-vx/c²)
(앞에서와 마찬가지로 ' 은 +x방향으로 등속 v로 이동하는 계에서 관측)
( γ = 1/root(1-v²/c²) )
여기서 포인트는, 정지한 S계와 +x방향으로 v로 이동하는 S'계의 시간이 다르다는 것입니다. ( t ≠ t' )
이것은, S계 사람이 S' 사람을 관측할때 시간이 다르게 느껴진다는 것이며, 그 달라지는 정도는 단순히 속도에만 관련된것이 아니라 위치 x와도 섞여있습니다.
이것을 가리켜 4-vector(포벡터)라고 부르며, 여기서 시간과 공간이 뒤섞이는 4차원의 개념이 등장한 것입니다.
문장으로 풀어서 쓰자면, 물체가 어떤 속도 v로 등속운동을 하면 그 물체의 위치좌표는 시간과 엮인값이다.(반대로 물체의 시간을 측정하면 물체가 있는 위치좌표와 엮인다) 이 되겠지요.
자세히보면 γ값은 v²/c² 이 v가 c에 근접할때 비로소 커지므로, 일상속도에서는 그 효과가 사라지는 것을 볼 수 있습니다. v가 작다면 v²/c² ~ 0 이고 그러면 γ~1 이되며 x' = x-vt, t' = t 이 되므로 갈릴리안 변환의 형태가 되는것을 알수있습니다.
포벡터는 별다른게 아니고, 본래의 x,y,z 에 새로운 항 t가 추가된 것이죠.
단위를 맞추기위해 (ct, x, y, z) 라고 표시합니다.
β = v/c 라고 하면 로렌츠변환은 다음과같은 행렬곱으로 간단히 표현될수 있습니다.
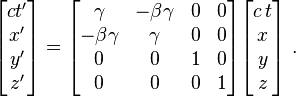
참고로 여기서 γ를 Lorentz factor 라고 부릅니다. 그리고 단위를 맞추기위하여 c를 곱해줬는데, 사실 이것은 인간이 정한 기준일 뿐입니다. 오히려 자연에서 자연스러운것은 c=1을 기준으로 잡는것이죠.
우리가 사용하고있는 시간 1초, 거리 1m 의 단위들은 우리 인간기준으로 정한것이니까요.
그래서 보통 c를 생략하고 쓰기도 합니다. 이것을 통일하려면 빛을 기준으로 잡으면 되죠.
즉, 거리로 통일시켜보면 시간1초에 해당하는 거리는 빛이 1초동안 진행하는 거리인 3*10^8 m 에 해당되며, 반대로 시간에 맞추면 거리 1m는 빛이 1m를 통과하는 시간인 1/3 * 10^-8 s 가 되겠죠.
이러한 로렌츠변환이 성립함에따라, 갈릴리안 변환의 수정이 일어났습니다.
즉, 모든 물리법칙은 갈릴리안 변환하에서 동일하게 관측된다 -> 라는 것에서,
모든 물리법칙은 로렌츠변환하에서 동일하게 관측된다 라고 말이죠. 로렌츠가 밝혀낸 것은 맥스웰방정식을 맞게하기위한 수정된 갈릴리안 변환식이며, 이 식의 의미를 밝혀낸 사람은 아인슈타인이었습니다.
그는 이것을 특수상대성 원리로 정리하여 발표하였는데, 다음과같은 두 문장으로 표현됩니다.
1. 모든 관성계에서 물리법칙은 동일하게 관측된다.
2. 모든 관성계에서 광속은 불변.
기존의 1.항목은 갈릴리안 변환을 내포하고있었지만, 이제는 로렌츠변환을 포함하고있죠. 지금껏 써오던 갈릴리안변환은 v가 느릴때의 근사치였던 것입니다.
이 특수상대성원리에서 그 유명한 twin paradox(쌍둥이 역설)을 비롯하여 여러 문제들이 제기되어왔는데,
지금껏 관측된 어떠한 현상도 이러한 특수상대성 원리를 위반하는 사례는 발견되지 않았습니다.
로렌츠 변환식에 의하면, 물체가 등속운동을 할때, 운동방향으로 Length contraction(길이단축)이 일어나며, 시간도 time dilation(시간지연)이 된다는 것인데, 이것을 증명한 결정적인 사례는 muon 이라는 입자에 의하여 밝혀졌습니다.
태양에서 생성되는 muon입자는 2.2 * 10^-6 초가 지나면 붕괴해버리는데, muon의 속도는 0.998c =0.998 * 3 * 10^8 m/s 이므로 life time동안 최대한 달려보아도 약 660m 밖에 이동하지 못합니다.
그러나, 지표면에 위치한 입자검출기에서도 muon이 관찰되는데, 그 이유는 다음과같습니다.
지구에있는 A가 뮤온을 관찰할때 : 뮤온이 광속에 근접한 속도로 이동하므로 time dilation에 의하여 뮤온의 시간이 느리게가는 것 처럼 보인다. 즉 뮤온의 수명이 늘어난것으로 관측되어 지표까지 이동 가능.
뮤온의 입장 : 태양에서부터 지구로 날아갈때 지구까지의 거리 L0가 length contraction이 일어나 줄어드므로 자신의 수명동안 충분히 갈수있는 거리가 된다.
여기서 중요한점은, 상대적 효과 라는 것입니다. 지구에서 보기에 뮤온은 분명 정해진 수명보다 오래사는것으로 관측되지만, 뮤온의 입장에서는 평소와 다를게 없는것입니다. 다만 길이단축이 일어나 조금만 움직여도 지구에 도달하게 되는것이지요.
그러나 이것을 착시- 같은 개념으로 이해하시면 안됩니다. 뮤온이 자각하지 못한것이지 지구에서 관측하면 분명 뮤온의 수명은 연장된것입니다. 그러나 실제로 뮤온의 수명이 연장된것이냐? 이러한 질문은 모순을 내포하고있습니다.
앞에서 절대속도를 정할수 없듯이, 뮤온의 수명에대한 절대적 기준이 없습니다. 다만 우리는 지구에 대하여 상대적으로 측정한 뮤온이 수명이 길어졌다 - 라고 결론을 내리는것이죠.
따라서 이러한 실험결과를 통하여 로렌츠변환이 틀림없다는 것을 증명하게 되었습니다.
또한 time dilation과 length contraction을 실제로 관찰하는 계기가 되었죠. 이 모든 효과는 Lorentz factor인 γ로 나타내어질수 있습니다. 정지상태에서 관찰한 것을 각각 t0, L0라고하면,
t = γt0
L = L0/r
로 나타내어집니다. v가 c에 근접할수록 γ는 점점 커지므로 t는 t0에비하여 커지고, L은 L0보다 작아지게되지요. 이렇게 정지 system에서 측정한 값을 proper value 라고 합니다.
t0는 proper time, L0는 proper length 가 되지요.
다시 원래의 벡터개념으로 돌아와보면, 3차원 벡터에서 (x,y,z) 일때, 스칼라량은 벡터의 크기인 root(x²+y²+z²) 으로 정의하였습니다. 아무리 좌표변환을 해보아도 벡터의 크기는 변하지 않죠.
즉, 스칼라의 정의는 좌표변환을 하였을때 불변이 되는 양인 셈인데, 위의 로렌츠변환에서는 스칼라가 다음과같은 양이 됩니다.(편의상 루트를 없앤 제곱의 형태를 취하겠습니다. 스칼라제곱도 스칼라이므로)
s² = c²t² - x² - y² - z²
이것을 interval(간격) 이라고 하며(지금은 간격의 제곱), 로렌츠변환하에서 불변하는 양입니다.
즉, P(ct, x, y, z) 에서 P'(c't', x', y',z') 으로 로렌츠변환이 일어났더라도 interval 값은 불변합니다.
수식으로 표현하면 c²t² - x² - y² - z² = c²t'² - x'² - y'² - z'² 라는 것이죠.
만약, c²t² < x²+y²+z² 이라면, s²이 음수가되면서 interval이 허수가 나오게 됩니다. 이것을 space-like(공간적) 이라 합니다. 이러한 사건들은 우리에게 영향을 끼칠수 없습니다.
만약, c²t² > x²+y²+z² 이라면 s는 실수가 나오게됩니다. 이것을 time-like(시간적)이라 하는데, 이 사건들은 우리에게 영향을 끼칠수 있습니다.
마지막으로, s=0, 즉 c²t² = x²+y²+z² 인 경우는 시간 t동안 공간좌표가 광속 * t 만큼 변했다는 것이죠. 즉 빛만이 이럴수 있습니다. 따라서 light-like 라고 합니다.
아래 그림을 보시면 이해가 빠를겁니다. light cone 라고 부르는 것인데..(출처-wikipedia)
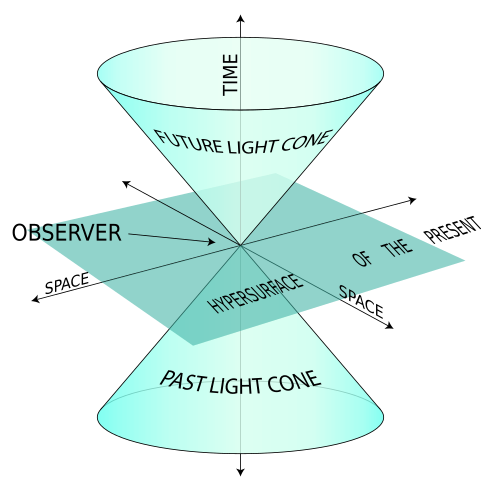
cone의 경계선이 빛에 해당됩니다. 원점을 지금 현재라고하면,
빛이 번쩍 했을때, 시간이지남에따라 cone의 위쪽모양처럼 빛이 퍼져나갈것이고,
그것의 past는 퍼져있던 빛이 모이는것이므로 cone의 아래쪽 모양처럼 되겠지요.
여기서 cone 바깥쪽에서 사건이 일어났다고하면, 그 사건은 지금 현재 우리에게 영향을 끼칠수 없습니다. 왜냐면 사건이 전달되는속도가 광속보다 작기때문이죠. 물론 충분한시간이 지나면 cone 안쪽으로 들어오면서 우리에게 영향을 줄수 있게됩니다. 이렇게 cone 바깥쪽의 사건들을 가리켜 spacelike 라고 합니다. 공간상으로 이격되어있기때문에 우리에게 영향을 줄수가 없습니다(지금 당장은)
예를들어보면, 지금 당장 태양이 사라졌다! 라는 사건은 spacelike에 해당되겠죠. 약 4분이 지나면 지구에 태양손실로인한 중력적효과로인한 궤도이탈을 비롯한 여러영향이 끼치는 것이죠.
그러나 cone 안쪽의 사건들은 아래쪽은 과거, 위쪽은 미래가 됩니다. 이러한 사건들은 우리에게 영향을 끼칠수있습니다. 영향을 끼친다기보다는 우리가 시간이 흐름에따라 위쪽cone의 안쪽을 이리저리 움직일때 조우할수 있다는 것이죠. 따라서 시간적으로 격리되어있으므로 timelike 에 해당됩니다. (단지 아직 일어나지않았을뿐- 이라는 개념)
두 사건모두 똑같이 시간이 흐르면 조우한다는 개념으로 이해하시면 안됩니다.
cone 바깥쪽의 future 사건은 우리가 아무리 cone안쪽에서 이리저리 움직여도 흘러도 조우할수가 없습니다.(수동적)
그러나 cone 안쪽의 future 사건은 cone 안쪽에서 이리저리 움직이다보면 충분히 조우할수 있죠.(능동적)
#. 참고사이트.
http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/spacetime/index.html
'Daily > Major' 카테고리의 다른 글
| Schrodinger Equation - Infinite Square Well(슈뢰딩거 방정식 무한포텐셜) (6) | 2012.04.18 |
|---|---|
| Schrodinger Equation(슈뢰딩거 방정식) - 기본 개념 (0) | 2012.04.18 |
| Inertia Tensor. (0) | 2011.12.12 |
| 외계행성의 생명체 존재여부? (2) | 2011.04.22 |
| Gradient, Divergence, Curl에 대하여. (21) | 2011.04.12 |



